Comprehension
A pencil maker ships pencils in boxes of size 50, 100 and 200. Due to packaging issues, some pencils break. About the 20 boxes he has supplied to a shop, the following information is available:
✦ Box no. 1 through 6 have 50 pencils, Box no. 7 through 16 have 100 pencils and Box no. 17 through 20 have 200 pencils.
✦ No box has less than 5% or more than 20% broken pencils.
Following is the frequency table of the number of broken pencils for the twenty boxes:
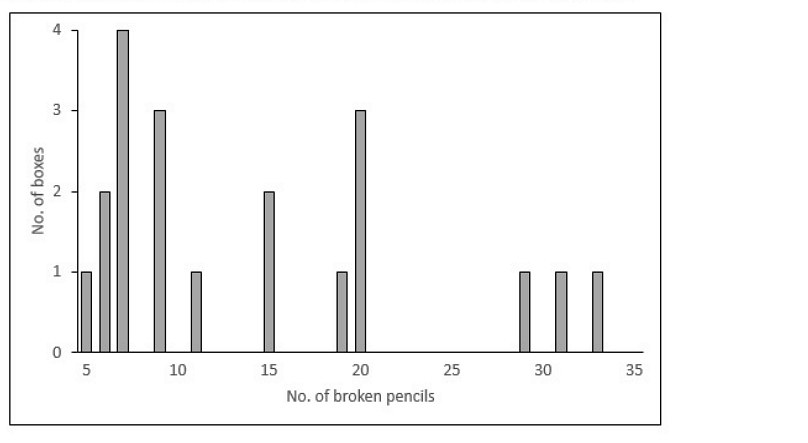
✦ Box no. 1 through 6 have 50 pencils, Box no. 7 through 16 have 100 pencils and Box no. 17 through 20 have 200 pencils.
✦ No box has less than 5% or more than 20% broken pencils.
Following is the frequency table of the number of broken pencils for the twenty boxes:
Question: 1
Which of the following can possibly be the sequence of the number of broken pencils in Boxes 7-16?
Which of the following can possibly be the sequence of the number of broken pencils in Boxes 7-16?
Updated On: Aug 9, 2024
- 5,7,7,7,9,11,15,20,20,20
- 7,7,9,9,11,13,15,19,20,20
- 7,7,7,7,11,15,15,19,20,20
- 5,6,6,6,11,15,15,20,20,20
- 6,7,9, 11,15,19,20,20,20,29
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The correct answer is option (C):7,7,7,7,11,15,15,19,20,20
Was this answer helpful?
0
0
Question: 2
Which of the following cannot be inferred conclusively from the given information?
Which of the following cannot be inferred conclusively from the given information?
Updated On: Aug 9, 2024
- No box numbered 1-6 has more broken pencils than any box numbered 17-20.
- Three among the boxes numbered 17 to 20 have 29, 31 and 33 broken pencils in some order.
- Four among the boxes numbered 7 to 16 have less than 10 broken pencils.
- Exactly three boxes have 20% broken pencils.
- A box with the highest percentage of broken pencils has 100 pencils.
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
The correct answer is option (D):Exactly three boxes have 20% broken pencils.
Was this answer helpful?
0
0
Question: 3
Suppose that additionally it is known that the number of broken pencils in Boxes 17-20 are in an increasing order. Which among the following additional information, if true, is not sufficient to uniquely know the number of defective pencils in each of the boxes numbered 17-20?
Suppose that additionally it is known that the number of broken pencils in Boxes 17-20 are in an increasing order. Which among the following additional information, if true, is not sufficient to uniquely know the number of defective pencils in each of the boxes numbered 17-20?
Updated On: Aug 9, 2024
- Box no. 17 contains more defective pencils than any box from among boxes no. 1-1d.
- Boxes no. 17-20 contain a total of 108 defective pencils.
- Boxes no. 7-16 contains a total of 124 defective pencils.
- Boxes no. 11-16 contain a total of 101 defective pencils.
- Boxes no. 7-16 contain a total of 133 defective pencils.
Hide Solution
Verified By Collegedunia
The Correct Option is
Solution and Explanation
The correct answer is option (E):Boxes no. 7-16 contain a total of 133 defective pencils.
Was this answer helpful?
0
0
Top Questions on Bar Graph
- Over the top (OTT) subscribers of a platform are segregated into three categories: i) Kid, ii) Elder, and iii) Others. Some of the subscribers used one app and the others used multiple apps to access the platform. The figure below shows the percentage of the total number of subscribers in 2023 and 2024 who belong to the 'Kid' and 'Elder' categories.
The following additional facts are known about the numbers of subscribers.
The total number of subscribers increased by 10% from 2023 to 2024.
In 2024, 1/2 of the subscribers from the 'Kid' category and 2/3 of the subscribers from the 'Elder' category subscribers use one app.
In 2023, the number of subscribers from the 'Kid' category who used multiple apps was the same as the number of subscribers from the 'Elder' category who used one app.
10,000 subscribers from the 'Kid' category used one app and 15,000 subscribers from the 'Elder' category used multiple apps in 2023. - An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day. The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below
The following information is known about ratings on Day 3.
1. 100 buyers gave product ratings on Day 3.
2. The modes of the product ratings were 4 and 5.
3. The numbers of buyers giving each product rating are non-zero multiples of 10.
4. The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3. - Six web surfers M, N, O, P, X, and Y each had 30 stars which they distributed among four bloggers A, B, C, and D. The number of stars received by A and B from the six web surfers is shown in the figure below
The following additional facts are known regarding the number of stars received by the bloggers from the surfers.
1. The numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0).
2. The total numbers of stars received by the bloggers were the same.
3. Each blogger received a different number of stars from M.
4. Two surfers gave all their stars to a single blogger.
5. D received more stars than C from Y - The chart below provides complete information about the number of countries visited by Dheeraj, Samantha and Nitesh, in Asia, Europe and the rest of the world (ROW).
The following additional facts are known about the countries visited by them.
1. 32 countries were visited by at least one of them.
2. USA (in ROW) is the only country that was visited by all three of them.
3. China (in Asia) is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha.
4. France (in Europe) is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh.
5. Half of the countries visited by both Samantha and Nitesh are in Europe. - Analyse the bar graph carefully and answer the following questions.
View More Questions
Questions Asked in XAT exam
- Consider a 4-digit number of the form abbb, i.e., the first digit is a (a > 0) and the last three digits are all b.
Which of the following conditions is both NECESSARY and SUFFICIENT to ensure that the 4- digit number is divisible by a?- XAT - 2024
- Number Systems
- FS food stall sells only chicken biryani. If FS fixes a selling price of Rs. 160 per plate, 300 plates of biriyani are sold. For each increase in the selling price by Rs. 10 per plate, 10 fewer plates are sold. Similarly, for each decrease in the selling price by Rs. 10 per plate, 10 more plates are sold. FS incurs a cost of Rs. 120 per plate of biriyani, and has decided that the selling price will never be less than the cost price. Moreover, due to capacity constraints, more than 400 plates cannot be produced in a day.
If the selling price on any given day is the same for all the plates and can only be a multiple of Rs. 10, then what is the maximum profit that FS can achieve in a day?- XAT - 2024
- Profit and Loss
- Read the following statement carefully.
___________like a fake can be a sign of___________, and clinging too tightly to what feels like one’s authentic self can ________that growth.
Fill in the blanks meaningfully, in the above statement, from the following options- XAT - 2024
- Fill in the Blanks
- Tech predictions often fail not because of wrong models or a lack of imagination, but due to lack of humility in admitting our uncertainty about the future.( Maximum 250 words )
- XAT - 2024
- Analytical Decision Making
- "Things which matter most must never be at the mercy of things which matter least."( Maximum 250 words)
- XAT - 2024
- Time Management
View More Questions