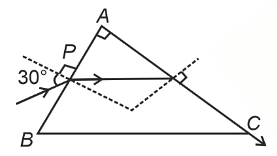
A light ray enters through a right angled prism at point P with the angle of incidence 30° as shown in figure. It travels through the prism parallel to its base BC and emerges along the face AC. The refractive index of the prism is :

- \(\frac{\sqrt5}{4}\)
- \(\frac{\sqrt5}{2}\)
- \(\frac{\sqrt3}{4}\)
- \(\frac{\sqrt3}{2}\)
The Correct Option is B
Solution and Explanation

Step 1: Relation in Prism
From the prism relation:
$$ r_1 + c = A $$
Rearranging for \( r_1 \):
$$ r_1 = 90^\circ - c \quad \text{...(1)} $$
Step 2: Expression for \( \cos c \)
We know:
$$ \sin c = \frac{1}{\mu} $$
Using trigonometric identity:
$$ \cos c = \frac{\sqrt{\mu^2 - 1}}{\mu} $$
Step 3: Apply Snell's Law on Incidence Surface
Using Snell’s law at the first surface:
$$ \sin 30^\circ = \mu \sin (r_1) $$
Substituting \( r_1 = 90^\circ - c \):
$$ \frac{1}{2} = \mu \sin (90^\circ - c) $$
Since \( \sin (90^\circ - c) = \cos c \), we get:
$$ \frac{1}{2} = \mu \times \frac{\sqrt{\mu^2 - 1}}{\mu} $$
Simplifying:
$$ \frac{1}{2} = \frac{\sqrt{\mu^2 - 1}}{1} $$
Step 4: Solve for \( \mu \)
Squaring both sides:
$$ \frac{1}{4} = \mu^2 - 1 $$
Rearranging:
$$ \mu^2 = \frac{5}{4} $$
Taking square root:
$$ \mu = \frac{\sqrt{5}}{2} $$
Conclusion
The refractive index \( \mu \) of the prism is \(\frac{\sqrt{5}}{2}\).
Top Questions on Refraction Through A Prism
- A laser beam of wavelength 500 nm and power 5 mW strikes normally on a perfectly reflecting surface of area 1 mm\(^2\) of a body. It rebounds back from the surface. Find the force exerted by the laser beam on the body.
- CBSE CLASS XII - 2025
- Physics
- Refraction Through A Prism
- A ray of light is incident on face AB of a prism ABC with angle of prism \( A \) and emerges out from face AC. The prism is set in the position of minimum deviation with angle of deviation \( \delta \). Find: \begin{enumerate} \item the angle of incidence and \item the angle of refraction on face AB. \end{enumerate}
- CBSE CLASS XII - 2025
- Physics
- Refraction Through A Prism
- Prove that total internal reflection of light ray from refracting surface is possible only when the value of angle of prism A be more than \(\sin^{-1}\left(\frac{1}{n}\right)\), where 'n' is refractive index of the material of prism.
- UP Board XII - 2025
- Physics
- Refraction Through A Prism
- (ii) Show ray diagram for the refraction of a light ray through a prism and point out the emergent angle and angle of deviation.
- UP Board X - 2025
- Science
- Refraction Through A Prism
- Derive Lens Maker's formula for a thin lens. Mention the effect of the refractive index and radius of curvature of the curved surfaces on the focal length of the lens.
- UP Board XII - 2025
- Physics
- Refraction Through A Prism
Questions Asked in NEET exam
- Two identical point masses P and Q, suspended from two separate massless springs of spring constants \(k_1\) and \(k_2\), respectively, oscillate vertically. If their maximum velocities are the same, the ratio of the amplitude of P to the amplitude of Q is :
- NEET (UG) - 2025
- Waves and Oscillations
A sphere of radius R is cut from a larger solid sphere of radius 2R as shown in the figure. The ratio of the moment of inertia of the smaller sphere to that of the rest part of the sphere about the Y-axis is :

- NEET (UG) - 2025
- Moment Of Inertia
- A microscope has an objective of focal length \(f_o = 2\) cm and an eyepiece of focal length \(f_e = 4\) cm. The tube length of the microscope is \(L = 40\) cm. If the distance of distinct vision of eye is \(D = 25\) cm, the magnification in the microscope is:
- NEET (UG) - 2025
- Optical Instruments
AB is a part of an electrical circuit (see figure). The potential difference \(V_A - V_B\), at the instant when current \(i = 2\) A and is increasing at a rate of 1 amp/second is:

- NEET (UG) - 2025
- Electromagnetic Induction and Inductance
- Twins are born to a family that lives next door to you. The twins are a boy and a girl. Which of the following must be true?
- NEET (UG) - 2025
- Genetics