Question:

$9.2\, g\, N_2O_4$ is heated in a $1L$ vessel till equilibrium state is established $N_2O_{4(g)} {<=>}2NO_{2(g)}$ In equilibrium state $50\% N_2O_4$ was dissociated, equilibrium constant will be (mol. wt. of $N_2O_4 = 92$)

Updated On: Jul 28, 2022

$0.3$
$0.2$
$0.1$
$0.4$

Hide Solution

Verified By Collegedunia

The Correct Option is B

Solution and Explanation

Moles of $N_{2}O_{4} =\frac{9.2}{92.0} =0.1$ mole $\begin{matrix}&N_{2}O_{4}& {<=>}&2NO_{2}(g)&&\\ \text{Initiailly }&0.1 {\text{moles}}&&0&\\ \text{At eqm.}&0.05&&0.05 \times 2 \end{matrix}$ $K=\frac{\left[NO_{2}\right]^{2}}{\left[N_{2}O_{4}\right]}$ $=\frac{0.1\times0.1}{0.05}$ $=0.2$

Was this answer helpful?

Top Questions on Law Of Chemical Equilibrium And Equilibrium Constant

For the reaction in equilibrium:
N₂(g) + 3H₂(g) ⇌ 2NH₃(g), ΔH = -Q
Reaction is favoured in forward direction by:
- NEET (UG) - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
View Solution
At a given temperature and pressure, the equilibrium constant values for the equilibria are given below:
\[ 3A_2 + B_2 \rightleftharpoons 2A_3B, \, K_1 \]
\[ A_3B \rightleftharpoons \frac{3}{2}A_2 + \frac{1}{2}B_2, \, K_2 \]
The relation between $ K_1 $ and $ K_2 $ is:
- NEET (UG) - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
View Solution
At $-20^\circ \text{C}$ and 1 atm pressure, a cylinder is filled with an equal number of $H_2$, $I_2$, and $HI$ molecules for the reaction:
\[H_2(g) + I_2(g) \rightleftharpoons 2HI(g)\] The $K_P$ for the process is $x \times 10^{-1}$.
$x = ___________)
Given: \(R = 0.082 \, \text{L atm K}^{-1} \text{mol}^{-1}$
- JEE Main - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
View Solution
The equilibrium $\mathrm{Cr_2O_7^{2-}} \rightleftharpoons 2\mathrm{CrO_4^{2-}}$ is shifted to the right in:
- JEE Main - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
View Solution
For the given hypothetical reactions, the equilibrium constants are as follows:
\[ X \rightleftharpoons Y; \, K_1 = 1.0 \]
\[ Y \rightleftharpoons Z; \, K_2 = 2.0 \]
\[ Z \rightleftharpoons W; \, K_3 = 4.0 \]
The equilibrium constant for the reaction
\[ X \rightleftharpoons W\]
is:
- JEE Main - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
View Solution

View More Questions

Concepts Used:

Law of Chemical Equilibrium

Law of Chemical Equilibrium states that at a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation.

Let us consider a general reversible reaction;

A+B ↔ C+D

After some time, there is a reduction in reactants A and B and an accumulation of the products C and D. As a result, the rate of the forward reaction decreases and that of backward reaction increases.

Eventually, the two reactions occur at the same rate and a state of equilibrium is attained.

By applying the Law of Mass Action;

The rate of forward reaction;

R_f = K_f [A]^a [B]^b

The rate of backward reaction;

R_b = K_b [C]^c [D]^d

Where,

[A], [B], [C] and [D] are the concentrations of A, B, C and D at equilibrium respectively.

a, b, c, and d are the stoichiometric coefficients of A, B, C and D respectively.

Kf and Kb are the rate constants of forward and backward reactions.

However, at equilibrium,

Rate of forward reaction = Rate of backward reaction.

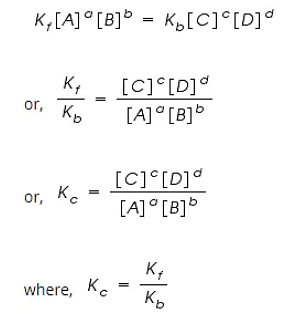
Kc is called the equilibrium constant expressed in terms of molar concentrations.

The above equation is known as the equation of Law of Chemical Equilibrium.