1 mole of HI is heated in a closed container of capacity of 2 L. At equilibrium half a mole of HI is dissociated. The equilibrium constant of the reaction is
1 mole of HI is heated in a closed container of capacity of 2 L. At equilibrium half a mole of HI is dissociated. The equilibrium constant of the reaction is
- 0.25
- 1
- 0.35
- 0.5
The Correct Option is A
Solution and Explanation
To determine the equilibrium constant of the reaction, we need to know the balanced equation for the dissociation of HI. The balanced equation is: 2HI ⇌ H2 + I2 The expression for the equilibrium constant (Kc) is given by the equation: Kc = [H2] * [I2] / [HI]2 Given that at equilibrium half a mole of HI is dissociated, we can calculate the equilibrium concentrations: [HI] = 0.5 mole / 2 L = 0.25 M [H2] = 0.5 * 0.25 M = 0.125 M [I2] = 0.5 * 0.25 M = 0.125 M Substituting these values into the equilibrium constant expression, we have: Kc = (0.125 M) * (0.125 M) / (0.25 M)2 Kc = 0.015625 / 0.0625 Kc = 0.25 Therefore, the equilibrium constant of the reaction is (A) 0.25.
Top Questions on Law Of Chemical Equilibrium And Equilibrium Constant
- For the reaction in equilibrium:
N2(g) + 3H2(g) ⇌ 2NH3(g), ΔH = -Q
Reaction is favoured in forward direction by:- NEET (UG) - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- At a given temperature and pressure, the equilibrium constant values for the equilibria are given below:
\[ 3A_2 + B_2 \rightleftharpoons 2A_3B, \, K_1 \]
\[ A_3B \rightleftharpoons \frac{3}{2}A_2 + \frac{1}{2}B_2, \, K_2 \]
The relation between \( K_1 \) and \( K_2 \) is:- NEET (UG) - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- At \(-20^\circ \text{C}\) and 1 atm pressure, a cylinder is filled with an equal number of \(H_2\), \(I_2\), and \(HI\) molecules for the reaction:
\[H_2(g) + I_2(g) \rightleftharpoons 2HI(g)\] The \(K_P\) for the process is \(x \times 10^{-1}\).
\(x = ___________)
Given: \(R = 0.082 \, \text{L atm K}^{-1} \text{mol}^{-1}\)- JEE Main - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- The equilibrium $\mathrm{Cr_2O_7^{2-}} \rightleftharpoons 2\mathrm{CrO_4^{2-}}$ is shifted to the right in:
- JEE Main - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- For the given hypothetical reactions, the equilibrium constants are as follows:
\[ X \rightleftharpoons Y; \, K_1 = 1.0 \]
\[ Y \rightleftharpoons Z; \, K_2 = 2.0 \]
\[ Z \rightleftharpoons W; \, K_3 = 4.0 \]
The equilibrium constant for the reaction
\[ X \rightleftharpoons W\]
is:- JEE Main - 2024
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
Questions Asked in KCET exam
- The speed of sound in an ideal gas at a given temperature T is v. The rms speed of gas molecules at that temperature is vrms. The ratio of the velocities v and vrms for helium and oxygen gases are X and X' respectively. Then \(\frac{X}{X'}\) is equal to
- KCET - 2023
- Thermodynamics
- If \(p(\frac{1}{q}+\frac{1}{r}),q(\frac{1}{r}+\frac{1}{p}),r(\frac{1}{p}+\frac{1}{q})\) are in A.P., then p, q, r
- KCET - 2023
- Arithmetic Progression
- A stretched wire of a material whose Young's modulus Y = 2 × 1011 Nm-2 has Poisson's ratio of 0.25. Its lateral strain εl = 10-3. The elastic energy density of the wire is
- KCET - 2023
- mechanical properties of solids
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Faradays laws of induction
- A 60 W source emits monochromatic light of wavelength 662.5 nm. The number of photons emitted per second is
- KCET - 2023
- Quantum Physics
Concepts Used:
Law of Chemical Equilibrium
Law of Chemical Equilibrium states that at a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation.
Let us consider a general reversible reaction;
A+B ↔ C+D
After some time, there is a reduction in reactants A and B and an accumulation of the products C and D. As a result, the rate of the forward reaction decreases and that of backward reaction increases.
Eventually, the two reactions occur at the same rate and a state of equilibrium is attained.
By applying the Law of Mass Action;
The rate of forward reaction;
Rf = Kf [A]a [B]b
The rate of backward reaction;
Rb = Kb [C]c [D]d
Where,
[A], [B], [C] and [D] are the concentrations of A, B, C and D at equilibrium respectively.
a, b, c, and d are the stoichiometric coefficients of A, B, C and D respectively.
Kf and Kb are the rate constants of forward and backward reactions.
However, at equilibrium,
Rate of forward reaction = Rate of backward reaction.
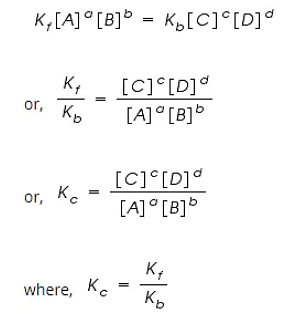
Kc is called the equilibrium constant expressed in terms of molar concentrations.
The above equation is known as the equation of Law of Chemical Equilibrium.